Sound coagulates particles in disperse system
|
|
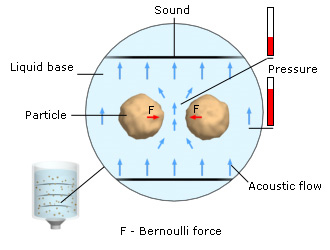
The pressure of the liquid base in the gap between the particles is less than the external pressure.
|
Synonym: acoustic coagulation
Implementing conditions
A sound beam should pass through a disperse system.
Effect indices
- The coagulation rate for the particles of a disperse system exposed to sound reaches a few hundreds of grams per second.
- The concentration reduction ratio for the particles of a disperse system exposed to sound reaches hundreds of times per second.
Description
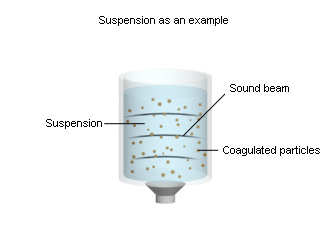
A beam of sound is passed through a layer of a disperse system, for example, a suspension. As a result, the suspension particles come close to each other, sticking together (coagulating). The particles become larger. They begin to settle down or come to the suspension surface. The phenomenon is called acoustic coagulation.
A suspension is a disperse system that consists of a liquid disperse medium (liquid base) and solid particles of more than 10–66 m in size. The suspension particles are in Brownian motion. However, they are large enough to resist the motion. If the density of the particles exceeds the density of the liquid base, they settle down (sediment) due to the gravity. Settling down, the particles coagulate. The sedimentation and coagulation proceed long enough.
Passing through the suspension, the sound beam initiates a number of processes in it, which make the suspension particles coagulate faster.
Firstly, the sound makes the suspension particles vibrate, thus increasing the diameter of their Brownian motion area. This raises the probability of collisions between the particles and, therefore, their coagulation rate.
Secondly, the sound pressure makes the particles drift away from the sound source. The concentration of particles in the suspension area which is the farthest from the sound source increases. This raises the probability of collisions between the particles and, therefore, their coagulation rate.
Thirldy, the sound produces acoustic flows in the liquid base (liquid) of the suspension. If the suspension particles are in the liquid flow or move relative to the liquid, they are acted upon by a Bernoulli force. This force moves the particles towards each other.
The liquid flow moves relative to the suspension particles. Flowing around two neighboring particles, the liquid changes its speed. The speed of the liquid in the gap between the particles increases. According to the Bernoulli law, an increase in the speed of a liquid with no change in its total flow decreases the pressure of the liquid. Thus, the pressure of the liquid in the gap exceeds the external pressure. A pressure difference arises in the liquid, producing a transverse Bernoulli force. This force makes the particles come close to each other, which increases their coagulation rate.
Note.
The illustration shows the final stage of acoustic coagulation.
Design models
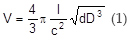
V — coagulation rate for particles of suspension exposed to sound, kg/s
Π — pi = 3.14
I — sound intensity, W/m2 (Watt/m2)
с — speed of sound in liquid base of suspension, m/s
d — average diameter of suspension particles, m
D — diameter of cross-section of sound beam, m
| Symbol | Dimensionality | Minimal | Maximal | Actual* |
| V | kg/s | 1.86 x 10–3 | ||
| I | W/m2 | 0 | 106 | 103 |
| с | m/s | 1180 | 1923 | 1497 |
| а | m | 10-7 | 10-4 | 10-6 |
| D | m | 0.1 | 10 | 1 |
*For suspension having liquid base.
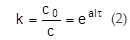
k — concentration reduction ratio for particles of suspension exposed to sound
c0 — initial concentration of particles in suspension before exposure to sound, kg/m3
c — concentration of particles in suspension after exposure to sound, kg/m3
а — empirical coefficient that depends on sound intensity, m2/(W•s)
I — intensity of sound in suspension, W/m2 (Watt/m2)
τ — time of exposure of suspension to sound, s
| Symbol | Dimensionality | Minimal | Maximal | Actual* |
| k | - | - | ~ 160 | |
| а | m2/(W•s) | 0.16 x 10–2 | 0.64 x 10–2 | 0.16 x 10–2 |
| I | W/m2 | 0 | 106 | 1.1 x 103 |
| τ | s | 0 | 100 | 3 |
Note.
- The coagulation rate determines the mass of particles coagulated in the suspension per unit time.
- Formula 2 assumes:
- the intensity of sound in the suspension is constant;
- the empirical coefficient a depends on the properties of the liquid, disperse particles and sound intensity;
- the concentration of particles decreases only after they settle down.
Experimental data
- To coagulate aerosols, use is made of a sound beam with an intensity more than 100 W/m2and frequency from 0,5 … 20 kHz. At sound intensity 104 W/m2 an aerosol gets coagulated within a few seconds.
- Aerosols are effectively purified by means of acoustic coagulation, if the aerosol concentration exceeds 1…2 g/m3.
- Ultrasound beams are used to coagulate hydrosols.
Reference.
Physical encyclopedia (5 volumes).article “Acoustic coagulation”. Prohorov A.M., ed. M., Sovetskaya entsiklopediya, 1992.
Properties
Sound speed c for liquids under normal conditions
| Liquid | s, m/s |
| Benzol | 1326 |
| Water | 1497 |
| Glycerin | 1923 |
| Kerosene 2) | 1295 |
| Transformer oil | 1425 |
| Mercury | 1453 |
| Ethyl alcohol | 1180 |
Empirical coefficient a versus sound intensity
| I, W/m2 | 67 | 600 | 1100 |
| a, m2/(W•s) | 0.64•10–2 | 0.15•10–2 | 0.16•10–2 |
Reference (for sound speed c).
Koshkin N.I., Shirkevich M.G. Handbook of elementary physics. M., Nauka, 1976, p. 105.
Application
-
Acoustic coagulation purifies gas from fine particles
> Acoustic coagulation purifies tobacco smoke from harmful admixtures
U.S. Patent 4,253,508; May 03,1981; “Selective filtering of tobacco smoke by enhanced filtration efficiency”. -
Acoustic coagulation purifies liquid from fine particles
> Acoustic coagulation purifies industrial waste water for reuse
U.S. Patent 5,466,367; Nov. 14,1995; “Industrial waste water treatment”.
Science: acoustics
Reference
Woodbury. Acoustical physics. New York: American Institute of Physics, 1993.
Hall, Donald E. Basic acoustics. Malabar, Fla.: Krieger, 1993.
Calvert, S., and H.M. Englund, eds. Handbook of Air Pollution Technology. New York: A Wiley–Interscience Publications, 1984.
Basic physics of ultrasound. Rockville, MD: The Center, Washington, 1983.
Urik, R.D. The Basis of Underwater Acoustics. New York: Pergamon Press, 1976.